思维100 奥数竞赛题

思维 $100$ STEM应用能力考试 由上海市科技传播学会主办，是一项让青少年灵活运用课内外科学知识，在科技、编程等方面训练动手实践和应用能力的科学普及活动，着重培养学生在 $STEM$ 领域中的综合应用能力，从而提高广大青少年的科学素质。
本文是 2024 年秋季思维100-五年级入围赛的竞赛题目和个人解答答案，根据学生回忆和部分机构发布的试题整理而成，与真题存在差异，仅供后续复习回顾之用。

第一部分

题目 1

$S(N)$ 表示正整数 $N$ 的数字之和，例如 $S(123) = 1 + 2 + 3 = 6$。若 $ p $ 是三位素数，满足 $S(p) = S(p^2)$，则 $p$ 的最小值为______。

点击查看答案

$p$ 的最小值为 199 。

#include <iostream>
#include <cmath>

int S(int n) {
    int sum = 0;
    while (n) {
        sum += n % 10;
        n /= 10;
    }
    return sum;
}

bool isPrime(int n) {
    if (n < 2) return false;
    if (n == 2) return true;
    if (n % 2 == 0) return false;
    for (int i = 3; i <= std::sqrt(n); i += 2) {
        if (n % i == 0) return false;
    }
    return true;
}

int main() {
    for (int p = 101; p <= 999; p += 2) {
        if (isPrime(p) && S(p) == S(p * p)) {
            std::cout << p << std::endl;
            break;
        }
    }
    return 0;
}

题目 2

将数字 $ 1、2、3、4、5、6、7、8、9 $ 随意填在一个圆周上，顺时针方向选取三个连续的数可以形成一个三位数。一共可以得到九个三位数，它们的和为______。

点击查看答案

答案为 4995 。

#include <iostream>
#include <vector>

int main() {
    int sum = 0;
    std::vector<int> digits = {1, 2, 3, 4, 5, 6, 7, 8, 9};
    for (int i = 0; i < 9; i++) {
        sum += digits[i] * 100 + digits[(i + 1) % 9] * 10 + digits[(i + 2) % 9];
    }
    std::cout << sum << std::endl;
    return 0;
}

题目 3

有两个质数 $X$ 和 $Y$，已知 $X < Y$，且 $X$ 和 $Y$ 的总和为 $128$。符合要求的 $(X, Y)$ 共有______种可能。

点击查看答案

答案为 3 , 分别为 $(19, 109)$, $(31, 97)$, $(61, 67)$ 。

#include <cmath>
#include <iostream>

bool isPrime(int n) {
    if (n < 2) return false;
    if (n == 2) return true;
    if (n % 2 == 0) return false;
    for (int i = 3; i <= std::sqrt(n); i += 2) {
        if (n % i == 0) return false;
    }
    return true;
}

int main() {
    int cnt = 0;
    for (int X = 2; X <= 63; X++) {
        int Y = 128 - X;
        if (isPrime(X) && isPrime(Y)) {
            std::cout << "(" << X << ", " << Y << ")" << std::endl;
            cnt++;
        }
    }
    std::cout << cnt << std::endl;
    return 0;
}

* 题目 4

原题目有一个 $9 \times 10$ 的方阵中有部分黑色区域，用 $2 \times 1$ 的瓷砖（瓷砖可以旋转）去覆盖这个方阵，要求所有瓷砖都正好覆盖 $9 \times 10$ 方阵中的两小格，黑色区域不能被覆盖住，而且两块瓷砖不能同时覆盖同一个小方格。最多能放入______块瓷砖。

此处为了方便绘制，用 1 表示黑色区域，0 表示白色区域，方阵抽象为一个 $9 \times 10$ 的矩阵，如下所示：

$$
\begin{bmatrix}
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{bmatrix}_{9 \times 10}
$$

点击查看答案

参考答案是 36 块瓷砖，暂无清晰讲解思路，后续补充。

题目 5

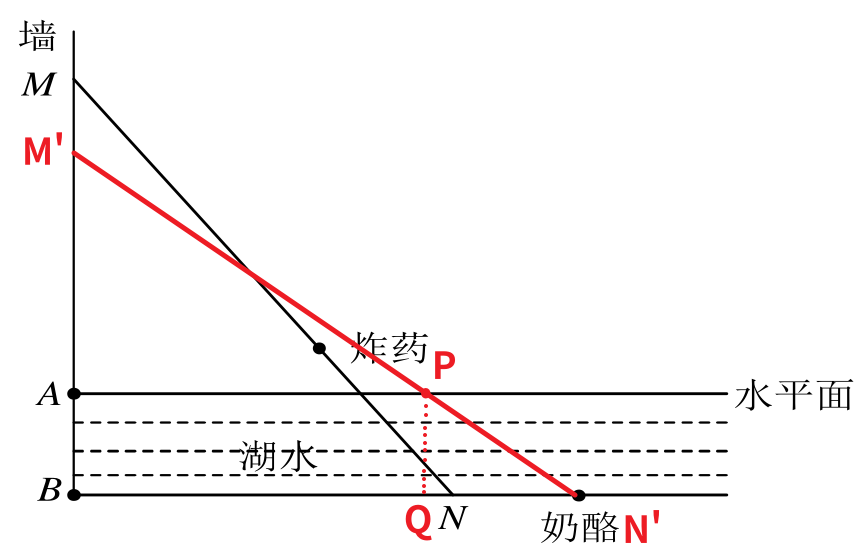
如下图，一堵墙垂直地竖立在湖边，湖水的深度 $AB$ 为 $10$ 分米。有一根木杆 $MN$ 的一端靠着墙上，另一端插在湖水中，$MN$ 的长度为 $50$ 分米。$MN$ 上靠近点 $N$ 的三等分点处绑了一个特殊的炸药，只要被浸没在湖水内部，炸药就会爆炸（在水平面边界上还不会爆炸）。一只水老鼠被绑在木杆的点 $N$ 处，它想去吃远处的奶酪，所以它会拉着木杆进行移动。为了能够吃到奶酪，并且不引爆炸药，那么奶酪离开墙的距离最多为______分米。

点击查看答案

奶酪离开墙的距离最多为 40 分米。

临界条件时如图中红色线段所示，此时水老鼠可以拉着木杆移动到最远处。

$\triangle BM’N’$ 与 $\triangle QPN’$ 相似，根据相似三角形原理：

$$
\frac{PN’}{PQ} = \frac{M’N’}{M’B} \Rightarrow M’B = \frac{M’N’ \cdot PQ}{PN’}
$$

其中 $M’N’ = MN = 50, PQ = AB = 10, PN’ = \frac{1}{3} \cdot MN = \frac{50}{3}$，代入计算得 $M’B = 40$。

在 $\triangle BM’N’$ 中，根据勾股定理：

$$
BN’ = \sqrt{M’N’^2 - M’B^2} = \sqrt{50^2 - 30^2} = 40
$$

题目 6

若 $a$、$b$、$c$ 都是大于 $1$ 的正整数，满足 $a + ab + abc = 415$，则 $c$ 的值为______。

点击查看答案

C 的值为 40 。

#include <iostream>

int main() {
    int a, b, c;
    for (a = 2; a < 415; ++a) {
        for (b = 2; b < 415; ++b) {
            for (c = 2; c < 415; ++c) {
                if (a + a * b + a * b * c == 415) {
                    std::cout << "a = " << a << ", b = " << b << ", c = " << c << std::endl;
                } 
            }
        }
    }
    return 0;
}

题目 7

有一排植物，它们的初始高度为 $1$ 厘米、$3$ 厘米、$5$ 厘米、$7$ 厘米、$9$ 厘米。有一种营养液可以使植物长高，但每次只能针对当前最矮的一棵植物，使它长高 $10$ 厘米。至少需要使用______次营养液，才会有一棵植物的高度不低于 $2024$ 厘米。

点击查看答案

至少需要使用 1008 次营养液。

#include <algorithm>
#include <iostream>
#include <vector>

int main() {
    std::vector<int> heights = {1, 3, 5, 7, 9};
    int targetHeight = 2024;
    int count = 0;

    while (*max_element(heights.begin(), heights.end()) < targetHeight) {
        auto minIt = std::min_element(heights.begin(), heights.end());
        *minIt += 10;
        count++;
    }

    std::cout << count << std::endl;
    return 0;
}

题目 8

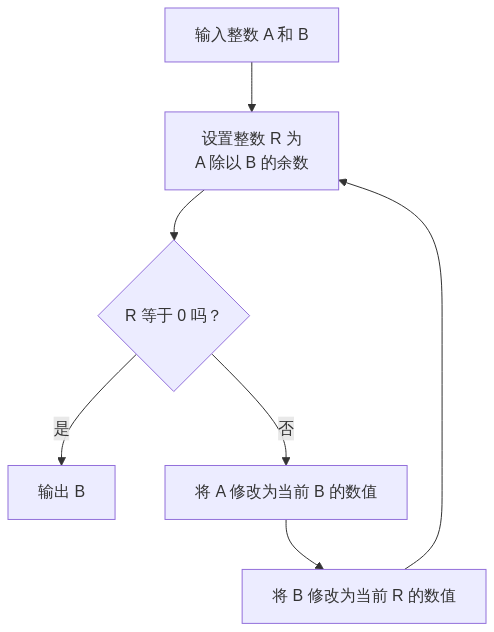
根据以下流程图，当输入数值 $A = 462$，$B = 2024$ 时，输出数值是______。

graph TD
    A[输入整数 A 和 B]
    B[设置整数 R 为 A 除以 B 的余数]
    C{R 等于 0 吗？}
    D[输出 B]
    E[将 A 修改为当前 B 的数值]
    F[将 B 修改为当前 R 的数值]

    A --> B
    B --> C
    C -->|是| D
    C -->|否| E
    E --> F
    F --> B

点击查看答案

答案是 $22$ 。

#include <iostream>

int main() {
    int A = 462, B = 2024;
    int R = A % B;
    while (R != 0) {
        A = B;
        B = R;
        R = A % B;
    }
    std::cout << B << std::endl;
}

题目 9

正方形 $ABCD$ 边长为 12，甲、乙两人沿着正方形的轮廓匀速行走。甲从 $A$ 出发顺时针行走，乙从 $B$ 出发逆时针行走，已知甲的速度是乙的 3 倍。他们第 10 次的相遇点为 $X$，第 2024 次的相遇点为 $Y$。线段 $AY$ 和 $BX$ 的交点是 $Z$，正方形被分成四块区域。这四块区域中，面积最小的区域的面积是______；面积最大的区域的面积是______。

点击查看答案

最小区域的面积是 $4.5$，最大区域的面积是 $85.5$，如下图所示：

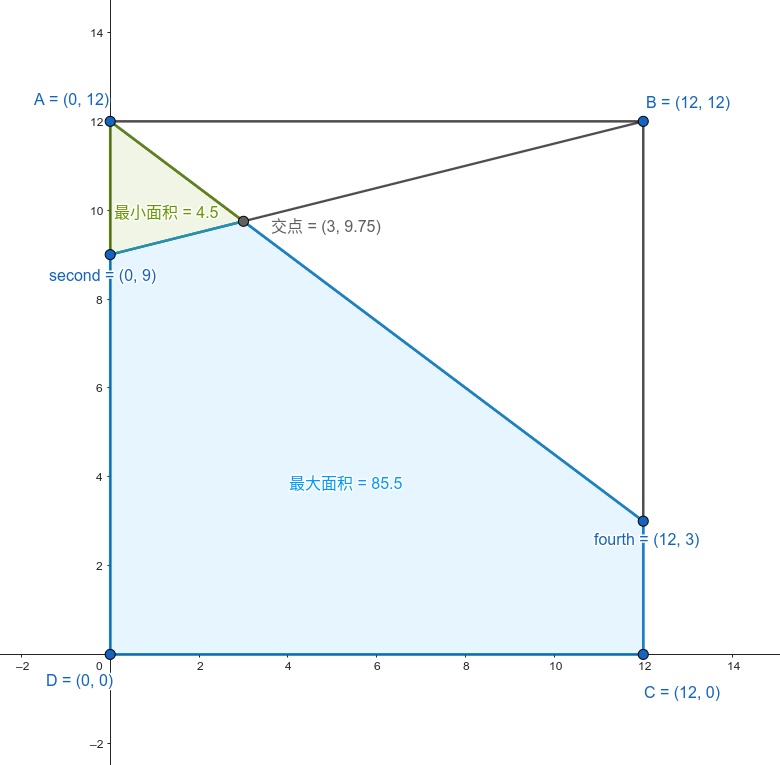
题目 10

将 5 个红球和 5 个蓝球排成一行，要求不存在三个相邻的同色球，不同的排法有______种。

点击查看答案

共有 84 种不同的排法。

#include <iostream>
#include <string>
#include <vector>
using namespace std;

void generateSequences(int red, int blue, string current, vector<string>& results) {
    if (red == 0 && blue == 0) {
        results.push_back(current);
        return;
    }

    if (red > 0) {
        if (current.size() < 2 || !(current[current.size() - 1] == 'R' && current[current.size() - 2] == 'R')) {
            generateSequences(red - 1, blue, current + 'R', results);
        }
    }

    if (blue > 0) {
        if (current.size() < 2 || !(current[current.size() - 1] == 'B' && current[current.size() - 2] == 'B')) {
            generateSequences(red, blue - 1, current + 'B', results);
        }
    }
}

int main() {
    int red = 5;
    int blue = 5;
    vector<string> results;

    generateSequences(red, blue, "", results);

    cout << "不同的排法有: " << results.size() << " 种。" << endl;

    return 0;
}

第二部分

第二部分是LeetCode经典题目 - 接雨水的衍生题目，题目难度为困难。

题目 1

给定一个长度为 $n$ 的非负整数数组 height，其中每个元素表示宽度为 1 的柱子的高度。例如给定 $height=[0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]$ 可视化为下面这张图，黑色部分为柱子。

在下了一场足够大的雨之后，柱子与柱子之间将承接一些雨水，图中的蓝色部分表示雨水。需要计算这些柱子可以承接多少单位的雨水。

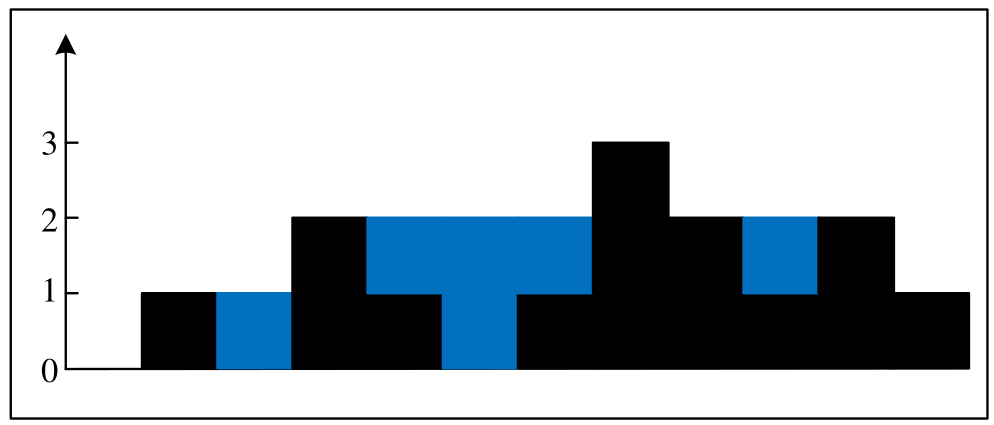
对于给定的数组，如何计算这些柱子排列能够接住多少单位的雨水？最直接的方法是先计算每一列雨水的高度（宽度都为 $1$），然后把所有雨水列的高度都加起来，就是所有雨水的容量了。

那如何计算每列雨水的高度呢？可以从图中看出，每一列雨水的高度，取决于该列左侧最高的柱子和右侧最高的柱子中，较矮的那个柱子的高度，与该列柱子高度的差。

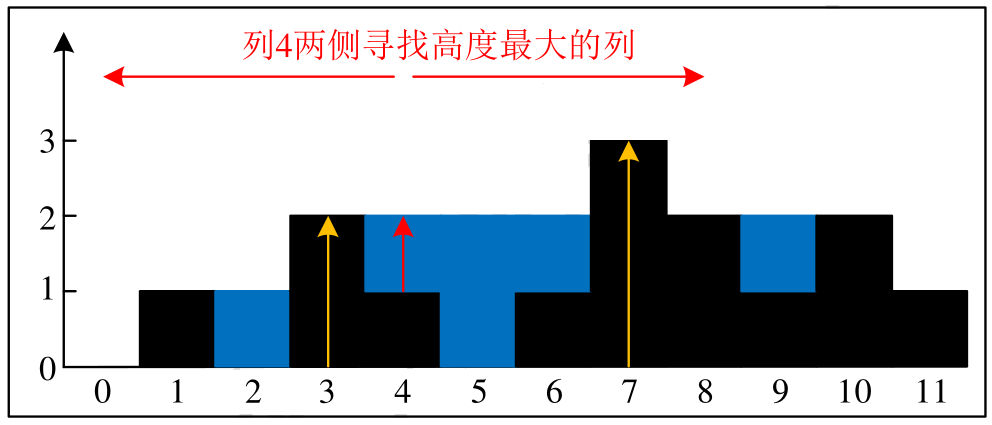
列 $4$ 左侧最高的柱子是列_______，高度为_______。

列 $4$ 右侧最高的柱子是列_______，高度为_______。

列 $4$ 柱子的高度为____________，所以列 $4$ 的雨水体积为___________。

题目 2

按照上一题的算法，当给定数组 $height=[4， 2， 0， 3， 2， 5]$ 时，计算出的雨水体积为__________。

题目 3

上面的暴力算法，随着数组中的元素数量增多，计算会变得复杂。现在我们用单调栈解法来优化这个算法。

单调栈就是不仅要保持栈的特性（先进后出），还要保证栈内元素有序。单调栈通常是一维数组。

如下图，只有比栈顶元素小的元素才能直接进栈，否则需要先将栈中比当前元素小的元素出栈，再将当前元素入栈。这样就保证了栈中保留的都是比当前入栈元素大的值，并且从栈顶到栈底的元素值是单调递增的。

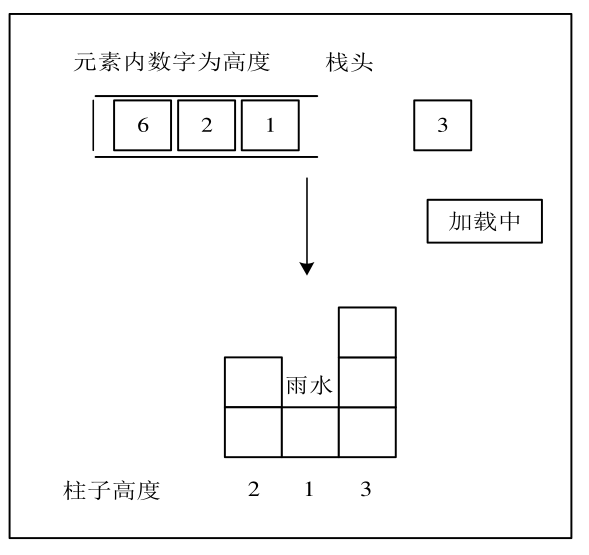
从栈头（元素从栈头弹出）到栈底的顺序是从小到大的顺序。其中栈中的数字表示柱子的高度，一旦发现添加的柱子高度大于栈顶元素了 (3>1)，就表明出现凹槽了，而栈头元素 $1$就是凹槽底部的柱子，如图中“雨水”的部分，栈头第二个元素就是凹槽左边的柱子 $2$，添加的元素 $3$ 就是凹槽右边的柱子。

栈里存放各个柱子的下标 index，通过下标即可通过访问数组 height 来得到柱子下标对应的高度。当我们遍历每一个柱子时，会出现三种情况：

3.1

（1）当前遍历的元素（柱子）高度小于栈顶元素的高度，此时要把这个元素________。

A. 弹出
B. 压入

3.2

（2）当前遍历的元素（柱子）高度等于栈顶元素的高度，此时要更新栈顶元素下标，因为遇到相同高度的柱子，需要使用最右边的柱子来计算宽度。

（3）当前遍历的元素（柱子）高度大于栈顶元素的高度，此时就出现凹槽了。

我们取栈顶元素，即将栈顶元素弹出，这个就是凹槽的底部，也就是中间雨水的位置，对应的下标记为 mid，对应的高度为 height[mid]（即为上图中的高度1）。此时的栈顶元素 st.top()，就是凹槽的左边位置，下标为 st.top()，对应的高度为 height[st.top()]。
当前遍历的元素i, 就是凹槽右边的位置, 下标为 i, 对应的高度为 height[i]（即为上图中的高度3）。则用 height[st.top()], height[i], height[mid] 表示的雨水高度为 min(height[st.top()], height[i]) - height[mid], 雨水的宽度为 i - st.top() - 1。

根据上述单调栈的算法，当输入为 $height=[3, 4, 1, 3, 3, 4, 1, 1, 3, 2, 3, 3]$ 时，能接住的雨水的体积是________。